数据结构与算法分析读书笔记系列05-散列

1. 前言
2. 一般想法
3. 散列函数
4. 分离链接
5. 开放定址法
6. 再散列
7. 可扩散列
8. 总结

1 前言

散列表的实现常常叫做（hashing）。散列是一种用于以常数平均时间执行插入、删除和查找的技术。但是，那些需要元素间任何排序信息的操作将不会得到有效的支持。因此，诸如FindMin、FindMax以及以线性时间将排过序的整个表进行打印的操作都是散列所不支持的。

2 一般想法

理想的散列表数据结构只不过是一个包含有关键字的具有固定大小的数组。每个关键字被映射到从0到TableSize-1这个范围中的某个数，并且被放到适当的单元中。这个映射就叫做散列函数（hash function），理想情况下它应该运算简单并且应该保证任何两个不同的关键字映射到不同的单元。

这就是散列的基本想法。剩下的问题则是要选择一个函数，决定当两个关键字散列到同一个值的时候（称为冲突（collsion））应该做什么以及如何确定散列表的大小。

3 散列函数

如果输入的关键字是整数，则一般合理的方法就是直接返回“key mod TableSize” 的结果，除非碰到具有某些不理想的性质。例如，表的大小是10，而输入的关键字都是以0结尾，在这种情况下散列函数的选择需要仔细考虑。为避免上面的那种情况，好的办法通常是保证表的大小是素数。

通常，关键字是字符串；在这种情形下，散列函数需要仔细饿选择。一般的选择方法是把字符串中字符的ASCII码值加起来。

另一个散列函数由图5-4表示。这个散列函数假设Key至少由两个字符外加NULL结束符。值27表示英文字母表的字母个数外加一个空格，而729=27² 。

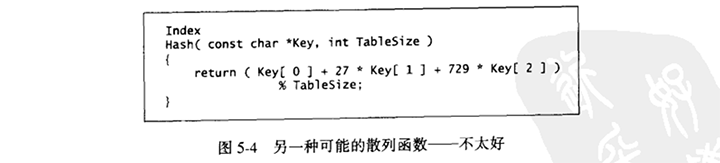
图5-5列出了散列函数的第3种尝试。这个散列函数涉及到关键字中所有字符，并且一般可以分布得很好（它计算Σ_i=0^KeySize-1 Key[KeySize - i - 1]•32ⁱ）,并将结果限制在适当的范围内）。程序根据Horner法则计算一个（32）多项式函数。

我们使用32是因为用32作乘法不是真的去乘，而是移动二进制，在程序第二行的加法可以用按位异或来代替。

图5-5所描述的散列函数就表的分布而言未必是最好的但是确实具有极其简单的优点。剩下的主要编程细节是解决冲突的消除问题。

4 分离链接

解决冲突的第一种方法通常叫做分离链接法（separate chaining），其做法是将散列到同一个值的所有元素保留到一个表中。

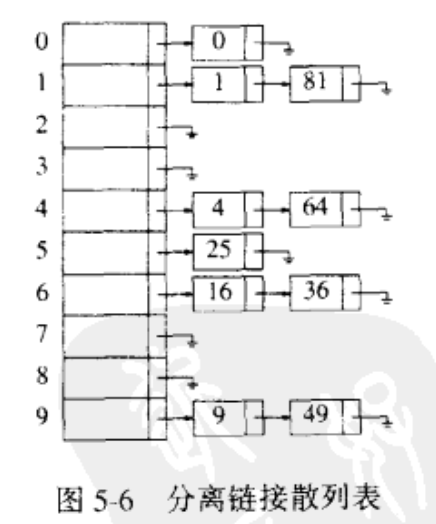
为执行Find，我们使用散列函数来确定究竟考查哪个表。此时我们以通常的方式遍历该表并返回所找到的被查找项所在的位置。

编程实现

除链表外，任何的方案都有可能用来解决冲突现象；一棵二叉查找树甚至另外一个散列表均可胜任，但是我们期望如果表大，同时散列函数好，那么所有的表就应该短，这样就不至于进行任何复杂的尝试。

我们定义散列表的装填因子（load factor）λ 为散列表中的元素个数与散列表大小的比值。表的实际大小实际上并不重要而装填因子才是重要的。分离链接散列的一般法则是使得表的大小尽量与预料的元素个数差不多（换句话说，让 λ ≈ 1）。正如前面提到的，使表的大小是素数以保证一个好的分布，这也是一个好的想法。

5 开放定址法

分离链接散列算法的缺点是需要指针，由于给新单元分配地址需要时间，因此这就导致算法的速度多少有些减慢，同时算法实际上还要求对另一种数据结构的实现。除使用链表解决冲突外，开放定址散列法（Open addressing hashing）是另外一种用链表解决冲突的方法。

在开发定址散列算法系统中，如果有冲突发生，那么就要尝试选择另外的单元，直到找出空的单元为止。更一般地，单元h₀ (X)，h₁ (X)，h₂ (X)，等等，相继被试选，其中h_i (X)=（Hash(X)+F(i)）mod TableSize，且F(0)= 0 。函数F是冲突解决方法。因为所有数据都要置入表内，所以开放定址散列法所需要的表要比分离链接散列用表大。一般来说，对于开放定址散列算法来说，装填因子应该低于 λ = 0.5。

5.1 线性探测法

在线性探测法中，函数F是i的线性函数，典型情形是F(i) = i。这相当于逐个探测每个单元（必要时可以绕回）以查找出一个空单元。只有表足够大，总能够找到一个自由单元，但是如此花费的时间是相当多的。更糟的是，即使表相对较空，这样占据的单元也会开始形成一些区块，其结果称为一次聚集（primary clustering），于是散列到区块的任何关键字都需要多次试选单元才能够解决冲突，然后该关键字被添加到相应的区块中。

如果表可以有多于一半被填满的话，那么线性探测就不是个好办法。然而，如果 λ = 0.5，那么插入操作平均只需要探测2.5次，并且对于成功的查找平均只需要探测1.5次。

5.2 平方探测法

平方探测是消除线性探测中一次聚集问题的冲突解决方法。平方探测就是冲突函数为二次函数的探测方法。流行的选择是F(i) = i² 。

对于线性探测，让元素几乎填满散列表并不是个好注意，因为此时表的性能会降低。对于平方探测情况甚至更糟：一旦表被填满超过一半，当表的大小不是素数时甚至在表被填满一半之前，就不能保证一次找到一个空单元了。同时有个定理，如果表有一半是空的，并且表的大小是素数，那么我们保证总能够插入一个新元素。

编程实现：

虽然平方探测排除了一次聚集，但是散列到同一个位置上的那些元素将探测相同备选单元。这叫做二次聚集（secondary clustering）。二次聚集是理论上的一个小缺憾。下面的技术将会排除这个缺憾，不过这要花费另外的一些乘法和除法。

5.3 双散列

对于双散列（double hashing），一种流行的选择是F(i) = i• hash₂ (X)。这个公式是说，我们将第二个散列函数应用到X并在距离hash₂ (X)，2hash₂ (X)等处探测。hash₂ (X)选择的不好将会是灾难性的。

如果双散列正确实现，则模拟表明，预期的探测次数几乎和随机冲突解决方法的情形相同。这使得双散列理论上很有吸引力。不过，平方探测不需要使用第二个散列函数，从而在实践中可能更简单并且更快。

6 再散列

对于使用平方探测的开放定址散列法，如果表的元素填的太满，那么操作的运行时间将开始消耗过长，且Insert操作可能失败。这可能发生在有太多的移动和插入混合的场合。此时，一种解决方案是建立另外一个大约两倍大的表（而且使用一个相关的新散列函数），扫描整个原始散列表，计算每个（未删除的）元素的新散列值并将其插入到新表中。

整个操作就叫做再散列（rehashing）。显然这是一种非常昂贵的操作；其运行时间为O(N)，因为N个元素要再散列的表的大小约为2N，不过，由于不是经常发生，因此实际效果根本没有这么差。

再散列可以用平方探测以多种方法实现。一种做法是只要表满到一半就再散列。另一种极端的方法是只有当插入失败时才再散列。第三种做法即途中（middle-of-the-load）策略：当表到达某个装填因子是进行再散列。由于随着装填因子的增加表的性能的确有下降，因此，以好的截止手段实现的第三种策略，可能是最好的策略。

7 可扩散列

本节最后讨论的是处理数据量太大以至于装不进主存的情况。正如我们前一节看到的，此时主要考虑的是检索数据所需的磁盘的存取次数。

如果使用开放定址散列法或分离链表散列法，那么主要的问题在于，在一次Find操作期间，冲突可能引起多个区块被考察，甚至对于理想分布的散列表也在所难免。不仅如此，当表变得过满的时候，必须执行代价巨大的到再散列这一步，它需要O（N）次磁盘访问。

一种聪明的选择叫做可扩散列（extendible hashing），它允许用两次磁盘访问执行一次Find。插入操作也需要很少的磁盘访问。

回忆上一节树的内容，B-树具有深度O（log_M/2 N）。随着M的增加，B-树的深度降低。理论上我们可以选择M非常大，使得B-树的深度为1.此时，在第一次以后的任何Find都将花费一次磁盘访问，因为推测根节点可能存在主存中。这种方法的问题在于分支系数（branching factor）太高，以至于为了确定数据在哪片树叶上要进行大量的处理工作。如果运行这一步的时间可以缩减，那么我们就将有一个实际的方案。这正是可扩散列使用的策略。

让我们假设，我们的数据有几个6比特整数组成。图5-23显示这些数据的可扩散列格式。用D代表根所使用的比特数，有时称其为目录（directory）。于是，目录中的项数为2^D 。d_L 为树叶L所有元素共有的最高位的位数。d_L 将依赖于特定的树叶，因此d_L ≤ D。

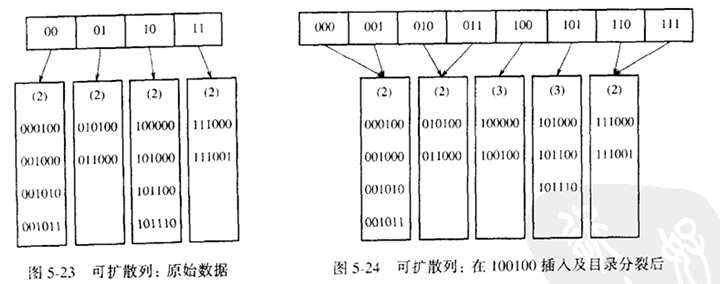
注意，所有未被分裂的树叶现在由两个相邻目录所指。因此，虽然整个目录被重写，但是其他树叶都没有实际被访问。

基于“位模式（bit pattern）是均匀分布的”这个合理的假设，经过非常复杂的分析可以得出可扩展散列的一些性能。

树叶的期望个数为（N/M）log₂ e。因此，平均树叶满的程度为ln2 = 0.69。这和B-树是一样的，其实这完全不奇怪，因为对于两种数据结构，当第（M+1）项被添加时，一些新的节点就建立起来。

更惊奇的结果是，目录的期望大小（换句话说即2^D）为O(N^{1 + 1/M}/M)。如果M很小，那么目录可能过分的大。在这种情况下，我们可以让树叶包含指向记录的指针而不是实际的记录，这样可以增加M的值。为了维持更小的目录，可以把第二个磁盘访问添加到每个Find操作中去。如果目录太大装不进主存，那么第二个磁盘访问怎么说也还是需要的。

8 总结

散列表可以用来以常数平均时间实现Insert和Find操作。当使用散列表时，注意诸如装填因子这样的细节是特别重要的，否则时间界将不在有效。当关键字不是短串或整数时，仔细选择散列函数也是很重要的。

对于分离链接散列法，虽然装填因子不很大时性能并不明显降低，但装填因子还是应该接近于1.对于开放定址散列算法，除法完全不可避免，否则装填因子不应该超过0.5。如果使用线性探测，那么性能随着装填因子接近于1将急速下降。再散列运算可以通过使表的增长（或者收缩）来实现，这样将会保持合理的装填因子。对于空间紧缺并且不可能申明巨大散列表的情况，这是很重要的。

散列有着丰富的应用。编译器使用散列表跟踪源代码中申明的变量。这种数据结构叫做符号表（symbol table）。散列表是这种问题的理想应用，因为只有Insert和Find要运行。标识符一般都不长，因此其散列函数能够迅速算出。

散列表对于任何图论问题都是有用的，在图论问题中，节点都有实际的名字而不是数字。

散列表的第三种常见的用途是在为游戏编制程序中，当程序搜索游戏的不同的行时，它跟踪通过计算基于位置的散列函数而看到一些位置。如果同样的位置再出现，程序通常通过简单移动变换来避免重复计算。游戏程序的这种一般特点叫做变换表（transposition table）。

散列的另一个用途是在线拼写检查程序。如果错拼检测（与正确性相比）更重要，那么整个目录可以被再散列，单词则可以在常数时间内被检测。散列表很适合这项工作，因为以字母顺序排列单词并不重要；而以它们在文件中出现的顺序显示出错拼写当然是可接受的。