数据结构与算法分析读书笔记系列04-树

Table of Contents

1 前言

对于大量的输入数据，链表的线性访问时间太慢，不宜使用。这部分介绍一种简单的数据结构，其大部分操作的运行时间平均O(logN)。

2 预备知识

定义树的一种自然的方式递归的方法。一棵树是一些节点的集合。这个集合可以是空集；若非空，则一棵树由称做根（root）的节点r以及0个或多个非空的（子）树T1 ,T2 ,…,Tk 组成，这些子树中每一棵的根都被来自根r的一条有向的边（edge）所连接。

每一棵子树的根叫做根r的儿子（child），而r是每一棵子树的根的父亲（parent）。

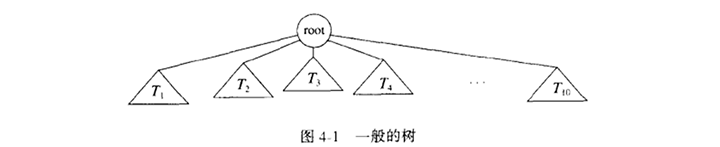
tree01.png

从递归的定义中我们发现，一棵树是N个节点和N-1条边的集合，其中的一个节点叫做根。没有儿子的节点称为树叶（leaf）；具有相同父亲节点的为兄弟（sibling），用类似的方法可以定义祖父（grandparent）和孙子（grandchild）关系。

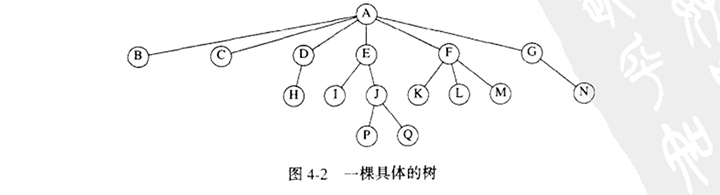
tree02.png

从节点n1 到ni 的路径（path） 定义为节点n1 ,n2 ,…,nk 的一个序列，使得1 ≤ i ≤ k，节点ni 是 ni+1 的父亲。这个路径的长（length）为该路径上边的条数，即k-1。从每一个节点到它自己有一条长为0的路径。注意，在一棵树中从根到每一个节点恰好存在一条路径。

对任意节点ni ，ni 的深度（depth）为从根到ni 的惟一路径的长。因此，根的深度为0。ni 的高（height）是从ni 到一片树叶的最长路径的长。因此所有树叶的高都是0。一棵树的高等于它的根的高。一个树的深度等于它的最深的树叶的深度；该深度总是等于这棵树的高。

2.1 树的实现

实现树的一种方法可以是在每一个节点除数据外还要有一些指针，使得该节点的每一个儿子都有一个指针指向它。

tree03.png

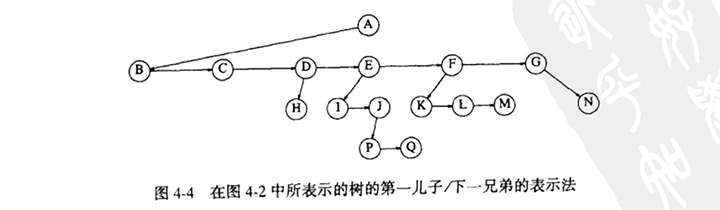
tree04.png

2.2 树的遍历和应用

流行的用法之一是包括UNIX、VAX/VMS和DOS在内的许多常用操作系统中的目录结构。

先序遍历（preorder traversal）。在先序遍历中，对节点的处理工作是在它的诸儿子节点被处理之前（pre）进行的。例子，列出分级文件系统中的目录。

后续遍历（postorder traversal）。在后序遍历中，对节点的处理工作是在它的诸儿子节点被计算后（post）进行的。例子，计算一个目录大小。

3 二叉树

二叉树（binary tree）是一棵树，其中每个节点都不能有多于两个的儿子。

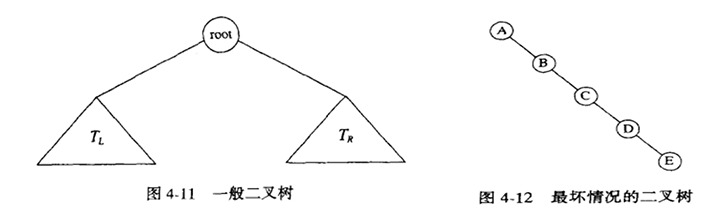
tree07.png

图4-11显示一棵由一个根和两棵子树组成的二叉树，TL 和 TR 均可能为空。

二叉树的一个性质是平均二叉树的深度要比N小得多，这个性质有时很重要。分析表明，这个平均深度我为O(\sqrt{N})，而对于特殊类型的二叉树，即二叉查找树（binary search tree），其深度的平均值是O(logN)。不幸的例子如图4-12所示，深度大到N-1。

3.1 实现

因为一棵二叉树最多有两个儿子，所以我们可以用指针直接指向它们。树节点的声明在结构上类似于双链表的声明，在声明中，一个节点就是由Key（关键字）信息加上两个指向其他节点的指针（Left和Right）组成的结构。

tree08.png

3.2 表达式树

表达式树的树叶式操作数（operand），而其它节点为操作符（operator）。

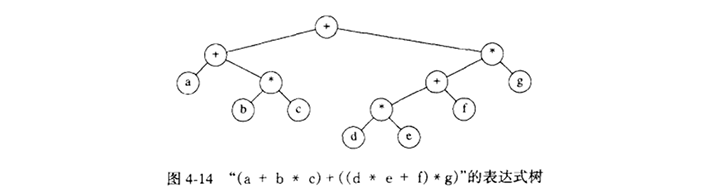
tree09.png

中缀表达式（infix expression）使用（左，节点，右）的中序遍历（inorder traversal）。

另一种遍历策略是递归打印左子树、右子树，然后打印运算符。这种策略称为后序遍历（postorder traversal）。

第三种遍历策略是先打印运算符，然后递归地打印出左右子树。是不常用的前缀（prefix）记法，这种遍历策略为先序遍历（preorder traversal）。

4 查找树ADT–二叉查找树

二叉查找树的性质是，对于树中的每个节点X，它的左子树中所有关键字值小于X的关键字值，而它的右子树中所有关键字值大于X的关键字值。

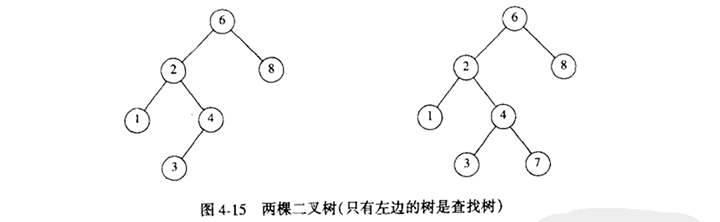
tree10.png

因为二叉查找树的平均深度是O(logN)，所以我们一般不必担心栈空间被用尽。

4.1 二叉查找树的编程实现

tree11.png

tree12.png

tree13.png

重复元的插入可以通过在节点记录中保留一个附加域以指示发生的频率来处理。

tree14.png

对于删除，复杂的情况是处理具有两个儿子的节点。一般的删除策略是用其右子树的最小数据（很容易找到）代替该节点的数据并递归地删除掉那个节点（现在它是空的）。 如果删除的次数不多，则通常使用的策略是懒惰删除（lazy deletion）：当一个元素要被删除时，它仍留在树中，而是只做了个被删除的记号。

tree15.png

4.2 平均情形分析

直观上，除MakeEmpty外，我们期望前一节所有的操作都花费log(N)时间，因为我们用常数时间在树中降低了一层，这样一来，对树的操作大致减少一半左右。因此，除MakeEmpty外，所有的操作都是O(d)，其中d是包含所访问的关键字的节点的深度。

一棵树的所有节点的深度的和称为内部路径长(internal path length)。

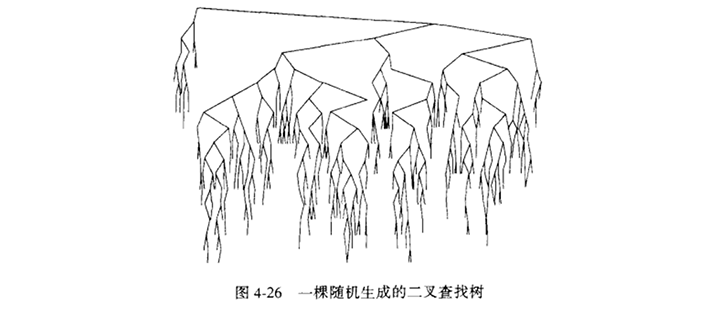
tree16.png

tree17.png

如果向一棵预先排序的树输入数据，那么一连串Insert操作将花费二次时间，而链表实际的代价会非常巨大，因为此时的树将只由哪些没有左儿子的节点组成。一种解决办法就是要有一个称为平衡（balance）的附加的结构条件：任何节点的深度均不得过深。有许多一般的算法实现平衡树，本节后面讨论最老的一种平衡查找树，即AVL树。

另外较新的方法是放弃平衡条件，允许树有任意深度，但是在每次操作之后要使用一个调整规则进行调整，使得后面的操作效率更高。这种类型的数据结构一般属于自调整（self-adjusting）类结构 。在二叉查找树的情况下，对于任意单个运算我们不在保证O(logN)的时间界，但是可以证明任意连续M次在最坏情形下花费O(MlogN)。一般这足以防止令人棘手的最坏情形。本节后面讨论的这种数据结构叫做伸展树（Splay Tree）。

5 AVL树

AVL(Adelson Velskii和Landis)树是带有平衡条件的二叉查找树。这个平衡条件必须容易保持，而且它须保证树的深度是O(logN) 。最简单的想法如图4-28所示左右子树具有相同高度。

另一种平衡条件是要求每个节点都必须要有相同高度的左子树和右子树。虽然这种平衡条件保证了树的深度小，但是它太严格，难以使用，需要放宽条件。

一棵AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树。空树的高度定为-1。可以证明，大致上讲，一个AVL树的高度最多为1.44log(N+2) - 1.328，但是实际上高度只比logN稍微多一些。

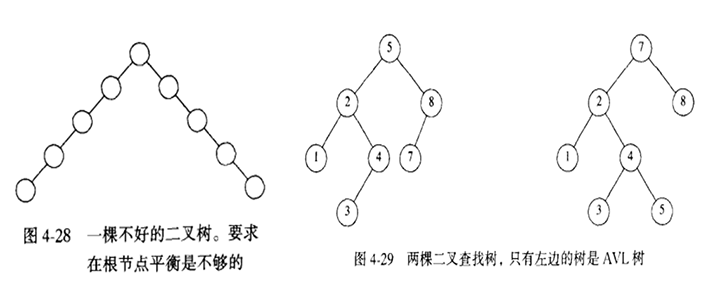
tree20.png

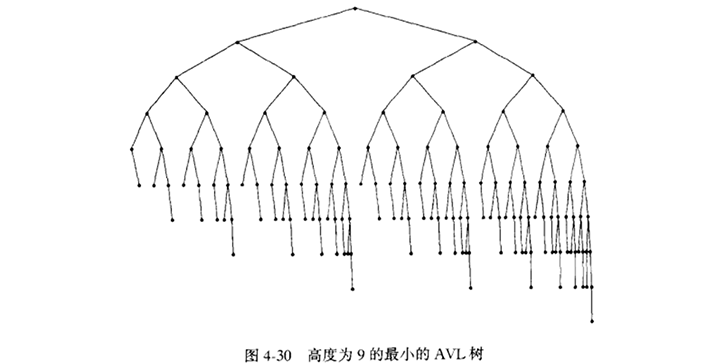
tree21.png

因此，除去可能的插入外（我们将假设懒惰删除），所有的树操作都可以以时间O(logN)执行。当进行插入操作时，我们需要更新通向根节点路径上哪些节点的所有平衡信息，而插入操作隐含着困难的原因在于，插入一个节点可能破坏AVL树的特性。发生这种情况，那么就要把性质恢复以后才认为这一步插入完成。事实上，这个总可以通过对树进行简单的修正来做到，我们称为旋转（rotation）。

在插入以后，只有那些从插入点到根节点的路径上的节点的平衡可能被改变，因为只有这些节点的子树可能发生改变。当我们沿着这条路径上行到根并更新平衡信息时，我们可以找到一个节点，它的新平衡破坏了AVL条件。我们将指出如何在第一个这样的节点（即最深的节点）重新平衡这棵树，并证明，这一重新平衡保证整个树满足AVL特性。

让我们把必须重新平衡的节点叫做α 。由于任意节点最多有两个儿子，因此高度不平衡时，α 点的两棵子树的高度差2。容易看出，这种不平衡可能出现在下面四种情况中:

  1. 对α 的左儿子的左子树进行一次插入。
  2. 对α 的左儿子的右子树进行一次插入。
  3. 对α 的右儿子的左子树进行一次插入。
  4. 对α 的右儿子的右子树进行一次插入。

情形1和情形4是关于α 点的镜像对称，而2和3是关于α 节点的镜像对称。因此，理论上只有两种情况，当然从编程的角度来看还是四种情形。

第一种情况是插入发生在“外边”的情况（即左-左或者右-右的情况），该情况通过对树的一次单旋转（single rotation）而完成调整。第二种情况是插入发生在“内部”的情形（即左-右或者右-左的情况），该情况通过稍微复杂些的双旋转（double rotation）来处理。我们将会看到，这些都是对树的基本操作，它们多次用于平衡树的一些算法中。

5.1 单旋转

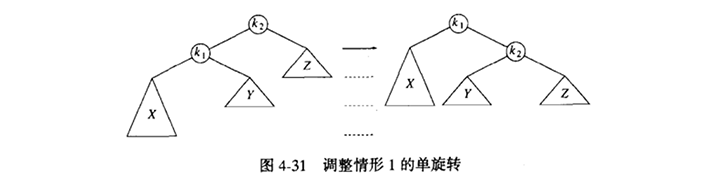
tree22.png

图4-31显示单旋转如何调整情形1。

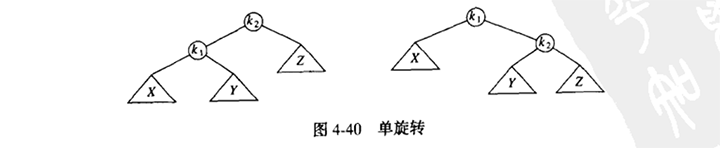
抽象的形容就是：把树形象的看成是柔软灵活的，抓住节点k1 ，闭上你的双眼，使劲的摇动它，在重力的作用下，k1 就变成了新的根。二叉查找树的性质告诉我们，在原树中k2 > k1 ，于是在新树中k2 变成了k1 的右儿子，X和Z仍然分别是k1 的左儿子和k2 的右儿子。

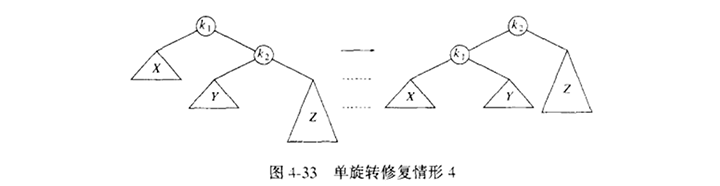
tree23.png

情形4代表一种对称的情形。图4-33指出单旋转如何使用。

5.2 双旋转

上面描述的算法有一个问题：如图4-34所示，对于情形2和情形3上面的做法无效。问题在于子树Y太深，单旋转没有降低它的深度。解决这问题的双旋转在图4-35中给出。

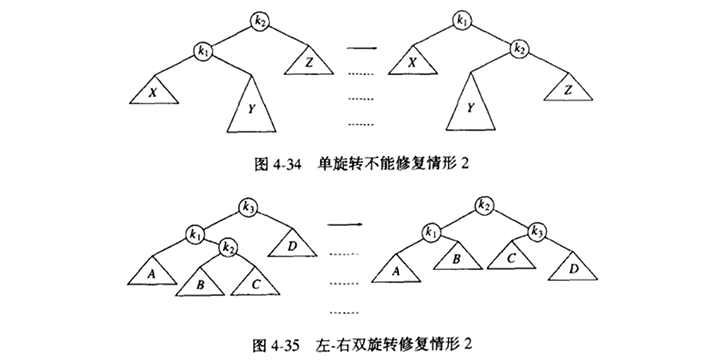
tree24.png

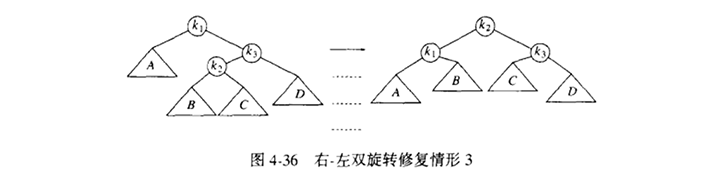
tree25.png

为了重新平衡，我们看到不能再让k3 作为根了，而图4-34所示的在k3 和k1 之间的旋转又解决不了问题，惟一的选择就是把k2 用作新的根。容易看出，最后得到的树满足AVL树的特性，与单旋转的情形一样，我们也把树的高度恢复到插入以前的水平，这就保证所有的重新平衡和高度更新是完善的。

5.3 编程实现

为将关键字是X的一个新节点插入到一棵AVL树中去，我们递归地将X插入到T的相应的子树（称为TLR ）中。如果TLR 的高度不变，那么插入完成。否则，如果T中出现高度不平衡，那么我们根据X以及T和TLR 中的关键字做适当的单旋转或双旋转，更新这些高度（并解决好与树的其余部分的连接），从而完成插入。由于一次旋转总能足以解决问题，因此仔细地编写非递归的程序一般来说要比编写递归程序快很多。然而，要想把非递归程序编写正确是相对困难的。

另一种效率问题涉及到高度信息的存储。。由于真正需要的实际上就是子树高度的差，应该保证它很小。

tree26.png

tree27.png

tree28.png

tree29.png

tree30.png

6 伸展树

伸展树（splay tree）,它保证从空树开始任意连续M次对树的操作最多花费O（MlogN）时间。

伸展树的基本想法是，当一个节点被访问后，它就要经过一系列AVL的旋转被放到根上。注意，如果一个节点很深，那么在其路径上就存在许多的节点也相对较深，通过重新构造可以使对所有这些节点的进一步访问所花费的时间变少。因此，如果节点过深，那么我们还要求重新构造应具有平衡这棵树（到某种程度）的作用。

6.1 一个简单的实现

实施上面描述的重新的构造的一种方法是执行单旋转，从下向上进行。这意味着我们将在访问路径上的每个节点和它们的父节点实施旋转。

虽然这个策略使得对k1 的访问花费时间减少，但是它并没有明显地改变（原先）访问路径上其他节点的状况。事实上可以证明，对于这种策略将会存在一系列M个操作共需要Ω (M*N)的时间，因此这个想法不够好。

6.2 展开

展开（Splaying）的思路类似于前面介绍的旋转的想法，不过在旋转如何实施上我们稍微有些选择的余地。

我们仍然从底部向上沿着访问路径旋转。令X是在访问路径上的一个（非根）节点，我们将在这个路径上实施旋转操作。如果X的父节点是树根，那么我们只要旋转X和树根。这就是沿着访问节点上的最后的旋转。否则，X就有父亲（P）和祖父（G）,存在两种情况以及对称的情形要考虑。第一种情况是之字型（zig-zag）情形（见图4-44）。这里，X是右儿子的形式，P是左儿子的形式（反之亦然）。如果是这种情况，我们就执行一次像AVL那样的双旋转。否则，出现另一种一字型（zig-zig）情形：X和P或者都是左儿子，或者都是右儿子。在这种情况下，我们把图4-45左边的树变换成右边的树。

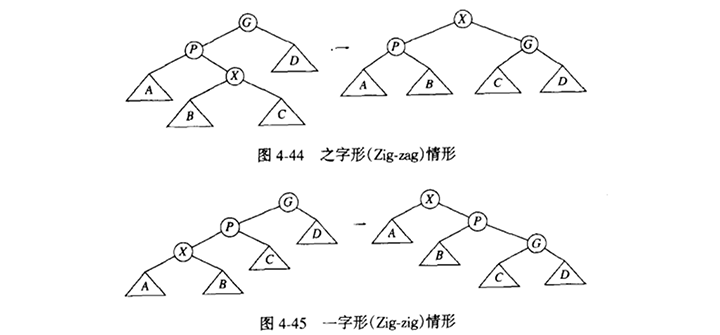
tree31.png

虽然从一些小例子很难看出来，但是展开操作不仅将访问的节点移动到根处，而且还把访问路径上大部分节点的深度大致减少一半的效果（某些浅的节点最多向下推后两个层次）。

我们可以通过访问要删除的节点实行删除操作。这种操作将节点上推到根处。如果删除该节点，则得到两棵子树TL 和TR （左子树和右子树）。如果我们找到TL 中最大的元素，那么这个元素就被旋转到TL 的根下，而此时TL 将有一个没有右儿子的根。我们可以是TR 为右儿子从而结束删除。

当访问路径太长而导致超出正常查找时间的时候，这些旋转将对未来的操作有益。当访问耗时很少的时候，这些旋转不那么有益甚至有害。对伸展树的分析很困难，因为树的结构经常变化。另一方面，伸展树的编程要比AVL树简单得多，这是因为要考虑的情形少并且没有平衡信息需要存储。

7 树的遍历

由于二叉查找树中对信息进行了排序，因而按照排序的顺序列出所有关键字会很简单。

tree32.png

图4-56的递归过程称为中序遍历。首先遍历左子树，然后当前的节点，最后遍历右子树。类似的还有先序遍历和后序遍历。第四种遍历用的很少，叫做层序遍历，在层序遍历中，所有深度为D的节点要在深度D+1的节点之前进行处理。层序遍历与其他类型的遍历不同的地方在于它不是递归地实施的；它用到队列，而不使用递归所默认的栈。

8 B-树

虽然迄今为止我们所看到的查找树都是二叉树，但是还有一种常用的查找树不是二叉树。这种树叫做B-树（B-tree）。

阶为M的B-树是一棵具有下列结构特性的树：

  • 树的根或者是一片树叶，或者其儿子树在2和M之间。
  • 除根外，所有非树叶节点的儿子树在[M/2]和M之间。
  • 所有的树叶都在相同的深度上。

所有的数据都存储在树叶上。(另一种流行的结构允许实际数据存储在树叶上，也可以存储在内部节点上，正如我们在二叉查找树中所做的那样。)

图4-58中的树是4阶B-树的一个例子。

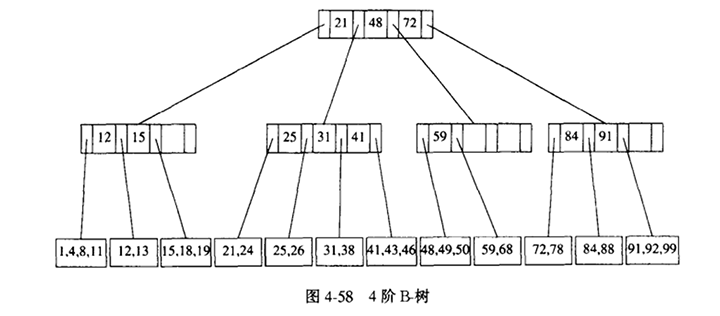
tree33.png

4阶B-树更流行的称呼是2-3-4树。而3阶B-树叫做2-3树。

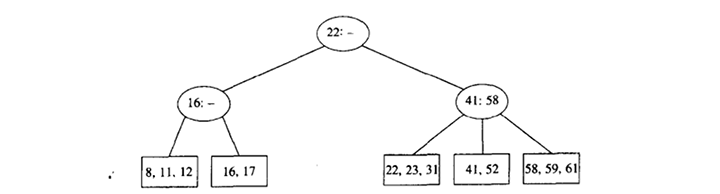
tree34.png

为了执行一次Find，我们从根开始并根据要查找的关键字与存储在节点上的两个（很可能是一个）值之间的关系确定（最多）三个方向中的一个方向。

当插入一个关键字的时候，只有在访问路径上的那些内部节点才有可能发生变化，

我们可以通过查找要被删除的关键字并将其除去而完成删除操作。

对于一般的M阶B-树，当插入一个关键字时，惟一的困难发生在接收该关键字的节点已经具有M个关键字的时候。这个关键字使得该节点具有M+1个关键字，我们可以把它分裂成两个节点，它们分别具有[(M+1)/2]个和[(M+1)/2]个关键字。由于这使得父节点多出一个儿子，因此我们必须检查这个节点是否可被父节点接受，如果父节点已经具备M个儿子，那么这个父节点就要被分裂成两个节点。我们重复这个过程直到找到一个父节点具有少于M个儿子，如果我们分裂根节点，那么我们就要创建一个新的根，这个根有两个儿子。

B-树的深度最多[logM/2 N]。在路径上的每个节点，我们执行O(logM)时间的工作量以确定选择哪个分支（使用折半查找），但是Insert和Delete可能需要O（M）的工作量来调整该节点上的所有信息。从运行时间考虑，M的最好（合法的）选择是M=3或M=4；当M再增大时插入和删除的时间就会增加。

B-树实际用于数据库系统，在那里树被存储在物理磁盘上而不是主存中。M的值选择为使得一个内部节点仍然能够装入一个磁盘区块的最大值，那么它一般说来是在32 ≤ M ≤ 256内。选择存储在一片树叶上的元素的最大个数时，要使得如果树叶是满的那么它就装满一个区块。这意味着，一个记录总可以在很少的磁盘访问中被找到，因为典型的B-树的深度只有2或3，而根（很可能还有第一层）可以放在主存中。

分析指出，一棵B-树将被占满ln 2= 69%。得到它的第（M+1）项时，例程不是总去分裂节点，而是搜索能够接纳新儿子的兄弟，此时我们就能更好的利用空间。

9 总结

本节介绍了树在操作系统、编译器设计以及查找中的应用。表达式树是所谓的分析树（parse tree）的小例子。分析树是编译器设计中的核心数据结构。分析树不是二叉树，而是表达式树相对简单的扩充。

查找树在算法设计中是非常重要的。它们几乎支持所有有用的操作，而其对数平均开销很小。查找树的非递归实现多少要快一些，但是递归实现更讲究、更精彩，而且易于理解和出错。

AVL树要求所有节点的左子树与右子树的高度相差最多是1。这就保证了树不至于太深。

在伸展树中的节点可以达到任意深度，但是在每次访问之后树又以多少有些神秘的方式被调整。实际效果是，任意M次操作花费O（MlogN）时间，它与平衡树花费的时间相同。

与2-路树或二叉树不同，B-树是平衡M-路树，它能很好的匹配磁盘；其特殊情形是2-3树，它是实现平衡查找树的另一种常用方法。

在实践中，所有平衡树方案的运行时间都不如简单的二叉查找树省时（差一个常数因子），但一般来说是可以接受的，它防止轻易得到最坏情形的输入。

给出一种O（NlogN）排序算法，通过将一些元素插入到查找树中然后执行一次中序遍历，我们得到的是排过序的元素。