数据结构与算法分析读书笔记系列09-图论算法
Table of Contents
1 前言
在这一部分,我们讨论几个一般的问题。这些算法不仅在实践中有用,而且因为在许多实际生活的应用中,若不仔细注意数据结构的选择将导致速度过慢,所以这些算法还是非常有趣的。
2 若干定义
一个图(graph)G = (V, E)由顶点(vertex)集V和边(edge)集E组成。每一条边就是一个点对(v, w),其中v,w ∈ V。有时也把边称做弧(arc)。如果点对是有序的,那么图就是有向的(directed)。有向的图有时也叫做有向图(digraph)。顶点v和w邻接(adjacent)当且仅当(v,w) ∈ E。在一个具有边(v, w)从而具有边(w, v)的无向图中,w和v邻接且v也和w邻接。有时候边还具有第三种成分,称为权(weight)或值(cost)。
图中的一条路径(path)是一个顶点序列w1 ,w2 ,w3 ,…, wN ,使得(wi , wi+1) ∈ E,1 ≤ i ≤ N。这样一条路径的长(length)是该路径上的边数,它等于N-1。从一个顶点到它自身可以看成是一条路径;如果路径不包含边,那么路径的长为0。这是定义特殊情形的一种方便的方法。如果图含有一条从一个顶点到它自身的边(v, v),那么路径v,v有时候叫做一个环(loop)。简单路径是其上所有顶点都是互异的,但是第一个顶点和最后一个顶点可能相同。
有向图中的圈(cycle)是满足w1 = wN 且长至少为1的一条路径;如果该路径是简单路径,那么这个圈就是简单圈。对于无向图,我们要求边是互异的。这些要求的根据在于无向图中的路径u,v,u不应该被认为是圈,因为(u, v)和(v, u)是同一条边。但是在有向图中它们是不同的边,因此它们为圈是有意义的。如果一个有向图没有圈,则称为无圈的(acyclic)。一个有向无圈图有时也简称为DAG。
如果在一个无向图中从每一个顶点到每个其他顶点都存在一条路径,则称该无向图是连通的(connected)。具有这样性质的有向图称为强连通的(strongly connected)。如果一个有向图不是强连通的,但是它的基础图(underly graph),即其弧上去掉方向所形成的图,是连通的,那么该有向图称为是弱连通的(weakly connected)。完全图(complete graph)是其每一对顶点都存在一条边的图。
航空系统和交通流都是可以用图模型化的例子。图论的应用,许多可能是相当巨大的,因此,我们使用的算法的效率是非常重要的。
图的表示
表示图的一种简单的方法是使用一个二维数组,称为邻接矩阵(adjacency matrix)表示法。对于每条边(u, v),我们置A[u][v] = 1;否则,数组的元素就是0。如果边有一个权,那么我们可以置A[u][v]等于该权,而使用一个很大或者很小的权作为标记表示不存在的边。虽然这么表示的优点是非常简单,但是空间需求大。
如果图不是稠密的(dense),换句话说,如果图是稀疏的(sparse),则更好的解决方法是使用邻接表(adjacency list)表示。对每个顶点,我们使用一个表存放所有邻接的顶点。
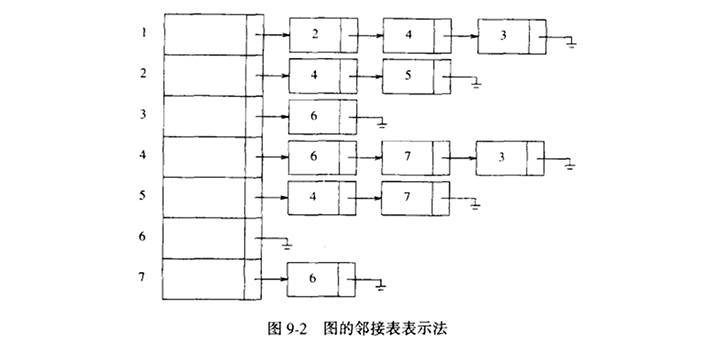
邻接表是表示图的标准方法。无向图可以类似的表示;每条边(u, v)出现在两个表中,因此空间的使用基本上是双倍的。在图论算法中通常需要找出与某个顶点v邻接的所有的顶点。而这可以通过简单地扫描相应的邻接表来完成,所用时间与这些顶点的个数成正比。
在大部分实际应用中顶点都有名字而不是数字,由于我们不能通过未知名字为一个数组做索引,因此我们必须提供从名字到数字的映射。一般通过散列表来完成这项工作。记录名字的另一种方法是使用字符串数组,但是当名字长,那就要花费大量的空间,因为顶点的名字要存两次。而使用散列表就要使用指针。
3 拓扑排序
拓扑排序是对有向无圈图的顶点的一种排序,它使得如果存在一条从vi 到vj 的路径,那么在排序中vj 出现在vi 的后面。显然,如果图含有圈,那么拓扑排序是不可能的。此外,排序不必是惟一的;任何合理的排序都是可以的。
一个简单的求拓扑排序的算法是先找出任意一个没有入边的顶点。然后我们显示出该顶点,并将它和它的边一起从图中删除。然后对图的其余部分应用同样的方法处理。

通过更仔细地注意该数据结构我们可以做得更好。运行时间长的原因在于对Indegree数组的顺序扫描。我们可以使用一个栈或者队列来进行优化。

如果使用邻接表,那么执行这个算法所用的时间为O(|E| + |V|)。for循环体对每条边顶多执行一次,队列操作对每个顶点最多进行一次,而初始化各步花费的时间也和图的大小成正比。
4 最短路径算法
这一节我们考查各种最短路径问题。输入是一个赋权图:与每条边(vi, vj)相联系的是穿越弧的代价(或称为值)ci,j。一条路径v1 v2 …vN 的值是∑i=1N-1ci,i+1 ,叫做赋权路径长(weighted path length)。而无权路径长(unweighted path length)只是路径上的边数,即N-1.
4.1 单源最短路径问题
给定一个赋权图G=(V, E)和一个特定的顶点s作为输入,找出从s到G中每一个其他顶点的最短赋权路径。
我们将考查求解该问题四种形态的算法。首先,我们要考虑无权最短路径问题并指出如何以O(|E| + |V|)时间解决它其次,我们还要介绍,如果假设没有负边,那么如何求解赋权最短路径问题。这个算法在使用合理的数据结构实现时的运行时间为O(|E|log|V|)。
如果图有负边,我们将提供一个简单的解法,不过它的时间界并不理想,为O(|E|• |V|)。最后,我们将以线性时间解决无圈图的特殊情形下的赋权的问题。
4.1.1 无权最短路径
利用广度优先搜索(breadth-first search),该方法按层处理顶点:距开始点最近的那些顶点首先被赋值,而最远的那些顶点最后被赋值,这很像对树的层序遍历(level-order traversal)。
图9-15显示该算法将要用到的记录过程的表的初始配置。
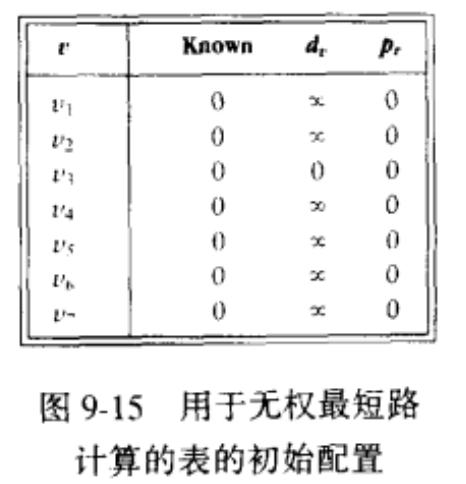
对于每个顶点,我们将跟踪三个信息,首先,我们把从s开始到顶点的距离放到dv 栏中。开始的时候,除s外所有的顶点都是不可达的,而s的路径长为0。pv 栏中的项为薄记变量,它将是我们能够显示出实际的路径。Known中的项在顶点被处理以后置为1。起初,所有的顶点都不是Known(已知的),包括开始顶点。当一个顶点被标记为已知时,我们就确信不会再找到更便宜的路径,因此对该顶点的处理实质上已经完成。
在任一时刻,只存在两种类型的未知顶点,它们的dv ≠ ∞ ,一些顶点的dv = CurrDist,而其余的则有dv = CurrDist + 1;对此可以使用队列对算法进行优化。


4.1.2 Dijkstra算法
如果图是赋权图,那么问题(明显地)就变得困难了,不过我们仍然可以使用来自无权情形的想法。
我们保留所有与前面相同的信息。因此,每个顶点或者标记为Known(已知)的,或者标记为unknown(未知)的。像之前一样,对于每个顶点保留一个临时距离dv 。这个距离实际上是使用已知顶点作为中间顶点从s到v的最短路径的长。和以前一样,我们记录pv ,它是引起dv 变化的最后的顶点。
解决单源最短路径问题的一般算法叫做Dijkstra算法(Dijkstra's algorithm)。这个有30年历史的解法是贪婪算法(greedy algorithm)最好的例子。贪婪算法一般地分阶段求解一个问题,在每个阶段它都能把当前出现的当作是最好的去处理。
Dijkstra算法像无权最短路径算法一样,按阶段进行。在每个阶段,Dijkstra算法选择一个顶点v,它在所有未知顶点中具有最小的dv ,同时算法申明从s到v的最短路径是已知的。阶段的其余部分由dw 值的更新工作组成。
在无权的情形,若dw = ∞ 则置 dw = dv + 1。因此,若顶点v能提供一条更短路径,则我们本质上降低了dw 的值。因此,若顶点v能提供一条更短路径,则我们本质上降低了dw 的值。我们对赋权的情形应用同样的逻辑,那么当dw 的新值dv + cc,w 是一个改进的值时我们就置dw = dv + cc,w 。简言之,使用通向w路径上的顶点v是不是一个好主意由算法决定。原始的值dw 是不用v的值;上面所算出的值是使用v(和仅仅那些已知的顶点)最便宜的路径。



利用反证法的证明可以证明,只要没有边的值为负,该算法总是能顺利完成。
如果使用不同的数据结构,那么Dijkstra算法可能会有更好的时间界。
4.1.3 具有负边值的图
如果图具有负边值,那么Dijkstra算法是行不通的。问题在于,一旦一个顶点u被申明是已知的,那就可能从某个另外的未知顶点v有一条回到u的负的路径。
我们把s放到队列中,然后,在每一个阶段我们让一个顶点v出队。找出所有与v邻接的顶点w,使得dw > dv + cc,w 。然后更新dw 和pw ,并在w不在队列中的时候把它放到队列中。可以为每个顶点设置一个比特位(bit)以指示它在队列中出现的情况。我们重复这个过程直到队列为空。

虽然如果没有负值圈该算法能够正常工作,但是第6行到第10行的代码每边执行一次的情况不在成立。每个顶点最多可以出队|V|次,因此,如果使用邻接表则运行时间是O(|E|• |V|)。这比Dijkstra算法多得多,幸运的是,实践中边的值是非负的。
4.1.4 无圈图
如果知道图是无圈的,那么我们可以通过改变申明顶点为已知的顺序,或者叫做顶点选择法则,来改进Dijkstra算法。新法则以拓扑顺序选择顶点。由于选择和更新可以在拓扑排序执行的时候进行,因此算法能够一趟完成。
因为当一个顶点v被选择以后,按照拓扑排序的法则,它没有从未知顶点发出的进入的边,因此它的距离dv 可以不再被降低,所以这种选择法则是行得通的。
使用这种选择法则不需要优先队列;由于选择花费常数时间,因此运行时间为O(|E| + |V|)。
无圈图的用途:模拟下坡滑雪、不可逆化学反应;更重要的用途是关键路径分析法。
事件节点图中每条边的松弛时间(slack time)代表对应动作可以被延迟而不推迟整体完成时间量。某些动作的松弛时间为零,这些动作是关键性动作,它们必须按计划结束。至少存在一条完全由零-松弛时间边组成的路径,这样的路径是关键路径(critical path)。
4.1.5 所有点对最短路径
利用动态规划计算有向图G=(V,E)中每一个点对间赋权最短路径的算法。
Dijkstra算法用于单出发点最短路径问题,该算法找出从任意一点s到所有其他顶点的最短路径。这个算法对稠密的图以O(|V|2) 时间运行,但是实际上对稀疏的图更快。我们将给出一个短小的算法解决对稠密图的所有点对的问题。这个算法的运行时间为O(|V|3) ,它不是对Dijkstra算法|V|次迭代的一种渐进改进但对非常稠密的图可能更快,原因是它的循环更紧凑。如果存在一些负的边值但是没有负值圈,那么这个算法也能正确运行;而Dijkstra算法此时是失败的。
Dijkstra算法的一些细节。算法在顶点s开始并分阶段工作。图中的每个顶点最终都要被选作中间顶点。如果当前所选顶点是v,那么对于每个w∊V,置dw = min(dw , dv + c(v,w))。这个公式是说,从s到w的最佳距离,或者是前面知道的从s到w的距离,或者是从s(最优地)到v然后再直接从v到w的结果。
从vi 到vj 只使用v1 ,v2 ,…, vk 作为中间顶点的最短路径或者根本不使用vk 作为中间顶点的最短路径,或者是由两条路径vi –> vk 和 vk –> vj 合并而成的最短路径,其中每条路径只使用前k-1个顶点作为中间顶点。得到下面的公式:D(k,i,j) = min{D(k-1,i,j),D(k-1,i,k) + D(k-1,k,j)},时间界还是O(|V|3)。
因为第k阶段只依赖第(k-1)阶段,所以看来只有两个|V|x|V|矩阵需要保存。然而,在用k开始或结束的路径上以k作为中间顶点对结果没有改进,除非存在一个负的圈。因此只有一个矩阵是必须的,因为D(k-1,i,k) = D(k,i,k) 和D(k-1,k,j) = D(k,k,j) ,这意味着右边的项都不改变值且都不需要存储。
该算法可以并行执行,因此这个算法很适合并行计算。
5 网络流问题
设给定边容量cv,w 的有向图G = (V, E)。这些容量可以代表通过一个管道的水的流量或在两个交叉路口之间马路上的交通流量。有两个顶点,一个是s,称为发点(source),一个是t,称为收点(sink)。对于任一条边(v, w),最多有流的cv,w 个单位可以通过。在既不是发点s又不是收点t的任一顶点v,总的进入的流必须等于总的发出的流。最大流问题就是确定从s到t可以通过的最大流量。例如,对于下面的图,左边的图,最大流是5,如右边的图所示。
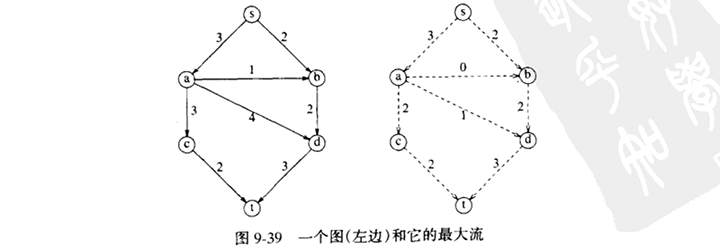
5.0.1 一个简单的最大流算法
解决这种问题的首要想法是分阶段进行。我们从图G开始并构造一个流图Gf 。Gf 表示在算法的任意阶段已经达到的流。开始时Gf 的所有的边都没有流,我们希望当算法终止时Gf 包含最大流。我们还构造一个图Gr ,称为残余图(residual graph),它表示对于每条边还能再添加多少流。对于每条边,我们可以从容量中减去当前的流而计算出残余的流。Gr 边叫做残余边(residual edge)。
在每个阶段,我们寻找图Gr 中从s到t的一条路径,这条路径叫做增长通路(augmenting path)。这条路径上的最小值边就是可以添加到路径每一边上的流的量。我们通过调整Gf 和重新计算Gr 做到这一点。当发现在Gr 中没有从s到t的路径时算法终止。
6 最小生成树
大体来说,一个无向图G的最小生成树就是由该图的那些连接G的所有顶点的边构成的树,且总价值最低。最小生成树存在当且仅当G是连通的。在最小生成树中边的条数为|V|-1。最小生成树是一棵树,因为它无圈;因为最小生成树包含每一个顶点,所以它是生成树。
对于任意生成树T,如果将一条不属于T的边e添加进来,则产生一个圈。如果从该圈中除去任意一条边在,则又恢复生成树的特性。如果边e的值比除去的边的值低,那么新的生成树的值就比原生成树的值低。如果在建立生成树时所添加的边在所有避免成圈的边中值最小,那么最后得到的生成树的值不能再改进,因为任意一条替代边的值都大于等于已经存在于该生成树中的一条边的值。它指出,对于最小生成树这种贪欲是成立的。下面介绍两种算法,它们的区别在于最小(值的)边的选取上。
6.0.1 Prim算法
计算最小生成树的一种方法是使其连续地一步步把长成。在每一步,都要把一个节点当作根并往上加边,这样也就把相关联的顶点加到增长的树上。
在算法的任一时刻,我们都可以看到一个已经添加到树上的顶点集,而其余顶点尚未加到这棵树中。此时,算法在每个阶段都可以通过选择边(u, v),使得(u, v)的值是所有u在树上但v不在树上的边的值中的最小值,而找出一个新的顶点并把它添加到这棵树中。
我们可以看到,Prim算法基本上和求最短路径的Dijkstra算法一样,因此和前面一样,我们对每一个顶点保留值dv 和pv 以及一个指标,标示该顶点是已知(known)的还是未知(unknown)的。这里,dv 是连接v到已知顶点的最短边的权,而pv 则是导致dv 改变的最后的顶点。
该算法整个实现实际上和Dijkstra算法的实现是一样的,对于Dijkstra算法分析所做的每一件事都可以用到这里。
6.0.2 Kruskal算法
第二种贪婪策略是连续地按照最小的权选择边,并且当所选的边不产生圈时就把它作为取定的边。
形式上,Kruskal算法是在处理一个森林——树的集合。开始的时候,存在|V|棵单节点树,而添加一边则将两棵树合并成一棵树。当算法终止的时候,就是一棵树了,这棵树就是最小生成树。
7 深度优先搜索的应用
深度优先搜索(depth-first search)是对先序遍历(preorder traversal)的推广。我们从某个顶点v开始处理v,然后递归地遍历所有与v邻接的顶点。

(全局)布尔型数组Visited[]初始化成false。通过只对那些尚未被访问的节点递归调用该函数,我们保证不会陷入无限的死循环。该方法保证每一条边只访问一次,所以只要使用邻接表,则执行遍历的总时间就是O(|E| + |V|)。
7.0.1 无向图
无向图是连通的,当且仅当从任一节点开始的深度优先搜索访问到每一个节点。
7.0.2 双连通性
如果一个连通的无向图的任一顶点删除之后,剩下的图仍然连通,那么这样的无向连通图就称为双连通的(biconnected)。
如果一个图是双连通的,那么,将其删除后图将不再连通的那些顶点叫做割点(articulation point)。这些节点在许多应用重视是很重要的。
深度优先搜索提供一种找出连通图中所有割点的线性时间算法。
7.0.3 欧拉回路
我们必须在图中找出一条路径使得该路径对图的每条边恰好访问一次。如果要解决“附加的问题”,那么我们就必须找到一个圈,该圈恰好经过每条边一次。这种图论问题在1736年由欧拉解决,它标志着图论的诞生。根据特定问题的叙述不同,这种问题通常叫做欧拉路径(Euler path,有时称欧拉环游——Euler tour)或欧拉回路(Euler circuit)问题。虽然欧拉环游和欧拉回路问题稍有不同但是却有相同的基本解。
可以观察到,其终点必须在起点上的欧拉回路只要当图是连通的并且每个顶点的度(即,边的条数)是偶数时才可能存在。如果恰好有两个顶点的度是奇数,那么当我们从一个奇数度的顶点出发最后终止在另一个奇数度的顶点时,仍然有可能得到一个欧拉环游。这里欧拉环游是必须访问图的每一边但最后不一定必须回到起点的路径。如果奇数度的顶点多于两个,那么欧拉环游也是不可能存在的。观察结果是必要也是充分条件。
7.0.4 有向图
利用与无向图相同的思路,也可以通过深度优先搜索以线性时间遍历有向图。如果图不是强连通的,那么从某个节点开始的深度优先搜索可能访问不了所有的节点。在这种情况下我们在某个未作标记的节点处开始,反复执行深度优先搜索,直到所有的节点都被访问到。
深度优先搜索的一种用途是检测一个有向图是否是无圈图,法则如下:一个有向图是无圈图当且仅当它没有背向边。拓扑排序也可以用来确定一个图是否是无圈图。进行拓扑排序的另一种方法是通过深度优先生成森林的后序遍历给顶点指定拓扑编号N,N-1,…,1。只要图是无圈的,这种排序就是一致的。
7.0.5 查看强分支
通过执行两次深度优先搜索,我们可以检测一个有向图是否是强连通的,如果它不是强连通的,那么我们实际上可以得到顶点的一些子集,它们到其自身是强连通的。
8 NP-完全性介绍
我们看到各种各样的图论问题的解法。所有这些问题都有一个多项式运行时间,除网络流问题外,运行时间或者是线性的,或者比线性多一些。
我们将看到,存在大量重要的问题,它们在复杂性上大体是等价的。这些问题形成一个类,叫做(NP-complete)问题。这些NP-完全问题精确的复杂度仍然需要确定并且在计算机理论科学方面仍然是最重要的开放性问题。要么所有这些问题有多项式时间解法,要么它们都没有多项式解法。
8.0.1 难与易
一方面,许多问题可以用线性时间求解。另一方面,确实存在某些真正难的问题。这些问题是如此的难,以至于它们不可能解出。正如实数不足以表示x2 < 0的解那样,可以证明,计算机不可能解决碰巧发生的每一个问题。这些“不可能”解出的问题叫做不可判定问题(undecidable problem)。
8.0.2 NP类
NP类在难度上逊于不可判定问题的类。NP代表 非确定多项式时间(nondeterministic polynomial-time) 。非确定性是非常有用的理论结构。此外,非确定性也不像人们想象的那么强大。例如,即使使用非确定性,不可判定问题仍然还是不可判定。
检验一个问题是否属于NP的简单方法是用"是/否(yes/no)问题"的语言描述该问题。如果我们在多项式时间内能够证明一个问题的任意“是”的实例是正确的选择。因此,对于哈密尔顿圈问题,一个“是”的实例就是图中任意一个包含所有顶点的简单的回路。由于给定一条路径,验证它是否真的是哈密尔顿圈是一件简单的事情,因此哈密尔顿圈问题属于NP。
由于解本身显然提供了验证方法,因此,NP类包括所有具有多项式解的问题。同时注意,不是所有的可判定问题都属于NP。没有人知道如何以多项式时间证明一个图没有哈密尔顿圈。似乎人们只能枚举所有的圈并且将它们一个一个地验证才行。因此,无哈密尔顿圈的问题不知属不属于NP。
8.0.3 NP-完全问题
在已知属于NP的所有问题中,存在一个子集,叫做NP-完全(NP-complete)问题,它包含了NP中最难的问题。NP-完全问题有一个性质,即NP中的任一问题都能够多项式地归约成NP-完全问题。
NP-完全问题是最难的NP问题的原因在于,一个NP-完全的问题基本上可以用作NP中任何问题的子程序,其花费只不过是多项式的开销量。因此,如果任意NP-完全问题有一个多项式时间解,那么NP中的每一个问题必然都有一个多项式时间的解。这使得NP完全问题是所有NP问题中最难的问题。
哈密尔顿回路问题、巡回售货员问题、最长路径问题都是NP-完全问题,此外,还有如装箱(bin packing)问题、背包(knapsack)问题、图的着色(graph coloring)问题以及团(clique)的问题都是著名的NP-完全问题。NP-完全问题相当广泛,包括来自操作系统(调度和安全)、数据库系统、运筹学、逻辑学、特别是图论等不同的领域的问题。
9 总结
在这一部分,介绍了图论的一些算法和生活中对应的一些实际模型。实际出现的图常常是非常稀疏的,因此,注意用于实现这些图的数据结构很重要。